Jednostavni kalkulator štednje - izračunajte iznos dospijeća pojedinca

O jednostavnom kalkulatoru uštede

Formula je navedena u nastavku:

Matematički se može izračunati za jednokratnu jednostavnu uštedu:

Drugo, ako se mjesečno napravi jednostavna ušteda, izračun:

Pri čemu,

• M je ukupan iznos na kraju jednostavnog razdoblja štednje
• Ja sam početni iznos uloženog
• i je fiksni iznos uložen u redovitim intervalima
• r je kamatna stopa
• F je učestalost plaćanja kamata
• n je broj razdoblja za koja će se ostvariti jednostavna ušteda.

Mnogo se banaka i drugih financijskih institucija natječe na tržištu kako bi privukli depozite kako bi mogli više poslovati, tj. Posuđivati ​​novac korporacijama ili pojedincima visoke neto vrijednosti. Neke bi banke plaćale višu kamatnu stopu ako depoziti prelaze određene granične vrijednosti i ako se vode na računu, ili će platiti standardnu ​​kamatnu stopu. Nadalje, mogla bi postojati razlika u učestalosti isplate kamata; na primjer, kamate se mogu složiti i isplaćivati ​​tromjesečno, polugodišnje ili godišnje, ovisno o banci. Stoga bi pomoću ovog kalkulatora pojedinci mogli odrediti koju bi financijsku instituciju trebali odabrati za ulaganje novca uspoređujući iznos dospijeća ili prinos zarađen na njihovim iznosima glavnice.

Kako izračunati jednostavnu uštedu?

Potrebno je slijediti korake u nastavku kako biste izračunali jednostavnu uštedu.

Korak # 1 - Utvrdite koliki bi iznos bio uložen, bez obzira radi li se o paušalnom fondu ili postoji povremeno ulaganje, a zatim bi to trebalo uzeti u obzir u usporedbi izračuna stopa uštede.

2. korak - shvatite kamatnu stopu koja je dostupna u opcijama za pojedinca, a koja bi se zaradila ili se očekuje da će se zaraditi jednostavnom uštedom.

Korak # 3 - Sada odredite razdoblje za koje će se investirati, a uglavnom će to biti dugoročno i ovisit će od slučaja do slučaja.

Korak # 4 - Podijelite kamatnu stopu s brojem razdoblja na koje se plaća kamata ili kamata Jednostavna štednja. Na primjer, ako je plaćena stopa 5% i plaća se mjesečno, tada bi kamatna stopa bila 5% / 12, što je 0,416%.

Korak # 5- Sada upotrijebite formulu o kojoj je gore bilo riječi u točki 1) u slučaju da se Jednostavna štednja napravi paušalno i upotrijebite formulu 2) u slučaju da se iznos Jednostavne štednje pravi u redovitim intervalima, zajedno s bilo kojim početnim iznosom za sve dostupne opcije .

Korak # 6 - Rezultat će biti iznos dospijeća koji uključuje i prihod od Jednostavne štednje i odabrao je onaj s najvećom isplatom u smislu kamata.

Primjer jednostavnog kalkulatora uštede

Gospodin William sada je punoljetan i uzbuđen je što će otvoriti svoj prvi štedni račun. Tražio je financijsku instituciju koja pruža visoku kamatnu stopu, ali zbunjen je jer ne shvaća koja će mu banka donijeti najveći povrat. Ispod su citati koje je gospodin William uvrstio u uži izbor.

Želi uložiti 1500 dolara u bilo koji od računa, a uložit će na način na koji račun plaća kamate. Na primjer, ako banka plaća polugodišnje, tada će se iznos ulagati jednako na kraju svakog razdoblja i nastavit će to činiti tijekom razdoblja od 10 godina.

Na temelju danih podataka trebate izračunati iznos koji bi on uštedio i kamate zarađene na istima te u koju bi banku odabrao ulaganje.

Riješenje:

Dajemo sljedeće detalje:

BANKA I

• I = Početni iznos bit će nula
• r = kamatna stopa koja iznosi 3,00%, a tromjesečno 3,00% / 4 što je 0,75%
• N = frekvencija koja je ovdje tromjesečna; dakle bit će 4
• n = broj godina jednostavne uštede, što je ovdje 10 godina.
• i = To je redoviti iznos koji treba uložiti, a to je 1500/4, to je 375 USD

Sada za izračunavanje iznosa dospijeća možemo koristiti donju formulu.

• = 0 * (1 + 0,75%) ^{10 * 4} + 375 * ((1 + 0,75%) ^{10 * 4} - 1 / 0,75%)
• = 17.417,43

Iznos dospijeća bit će 17.417,43

Složena zarađena kamata iznosila bi 17.417,43 USD - (375 * 40) = 2.417,43 USD.

BANKA II

• I = Početni iznos bit će nula
• r = kamatna stopa koja iznosi 3,12%, a polugodišnje će biti 3,12% / 2 što je 1,56%.
• N = Učestalost koja je ovdje polugodišnje, stoga će biti 2
• n = broj godina jednostavne uštede, što je ovdje 10 godina.
• i = To je redoviti iznos koji treba uložiti, a to je 1500/2, odnosno 750 USD

Sada za izračunavanje iznosa dospijeća možemo koristiti donju formulu.

• = 0 * (1 + 1,56%) ^{10 * 2} + 750 * ((1 + 1,56%) ^{10 * 2} - 1) / 1,56%
• = 17.445,58 USD

Vrijednost dospijeća bit će 17.445,58 USD

Složena zarađena kamata iznosila bi 17.445,58 USD - (750 USD * 20) = 2.445,58 USD.

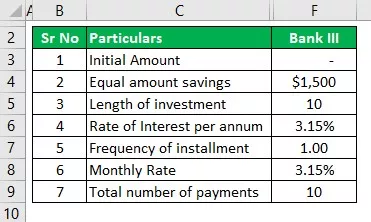
BANKA III

• I = Početni iznos bit će nula
• r = kamatna stopa koja iznosi 3,15%, a godišnje će biti 3,15% / 1, što je 3,15%
• N = Frekvencija koja je ovdje godišnje, stoga će biti 1
• n = broj godina jednostavne uštede, što je ovdje 10 godina.
• i = To je redoviti iznos koji treba uložiti, a to je 1500/1 za 1.500 USD

Sada za izračunavanje iznosa dospijeća možemo koristiti donju formulu.

• = 0 * (1 + 3,15%) ^{10 * 1} + 1500 * ((1 + 3,15%) ^{10 * 1} - 1) / 3,15%
• = 17.315,08 USD

Iznos dospijeća iznosit će 17.315,08 USD

Složena zarađena kamata iznosila bi 17.315,08 USD - (1500 $ * 10) = 2.315,08 USD.

Najviši zarađeni iznos je u Banci II, pa bi stoga trebao otvoriti račun u Banci II.

Zaključak

Ovaj kalkulator, kao što je gore spomenuto, može se koristiti za usporedbu različitih iznosa dospijeća u financijskoj instituciji jer viša kamatna stopa ne jamči najveći apsolutni iznos, kao što je vidljivo u gornjem primjeru. Stoga treba izračunati i usporediti iznose po dospijeću, a zatim donijeti odluku.