Što je koeficijent korelacije?
Koeficijent korelacije koristi se da bi se utvrdilo koliko je jak odnos između dvije varijable i njegove vrijednosti mogu se kretati od -1,0 do 1,0, gdje -1,0 predstavlja negativnu korelaciju, a +1,0 predstavlja pozitivan odnos. Razmatra relativna kretanja u varijablama, a zatim definira postoji li veza između njih.
Formula koeficijenta korelacije
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Gdje
- r = koeficijent korelacije
- n = broj promatranja
- x = 1 st varijabla u kontekstu
- y = 2. varijabla
Obrazloženje
Ako postoji bilo kakva korelacija ili recimo odnos između dvije varijable, tada će naznačiti ako se jedna od varijabli promijeni u vrijednosti, tada će i druga varijabla težiti promjeni vrijednosti, recimo u određenoj koja bi mogla biti u istoj ili u suprotnom smjeru. Numerički dio jednadžbe provodi test i relativnu snagu varijabli koje se kreću zajedno, a nazivnički dio jednadžbe skalira brojilac množenjem razlika varijabli s kvadratnim varijablama.
Primjeri
Primjer # 1
Uzmite u obzir sljedeće dvije varijable, x i y, koje trebate izračunati koeficijent korelacije.
Ispod su navedeni podaci za izračun.

Riješenje:
Koristeći gornju jednadžbu, možemo izračunati sljedeće

Sve vrijednosti imamo u gornjoj tablici s n = 4.
Unesite sada vrijednosti za izračun koeficijenta korelacije.

Stoga je izračun sljedeći,

r = (4 * 25,032,24) - (262,55 * 317,31) / √ ((4 * 20,855.74) - (262,55) 2 ) * ((4 * 30,058,55) - (317,31) 2 )
r = 16.820,21 / 16.831,57
Koeficijent će biti -

Koeficijent = 0,99932640
Primjer # 2
Zemlja X je zemlja s rastućom ekonomijom i želi provesti neovisnu analizu odluka koje donosi njezina središnja banka u vezi s promjenama kamatnih stopa, jesu li one utjecale na inflaciju i ima li središnja banka mogućnost da to kontrolira.
Slijedeći sažetak kamatne stope i stope inflacije koja je u prosjeku vladala u zemlji tih godina dani su u nastavku.
Ispod su navedeni podaci za izračun.

Predsjednik zemlje obratio vam se kako biste na sljedećem sastanku proveli analizu i održali prezentaciju o istoj. Koristite korelaciju i utvrdite je li središnja banka ispunila svoj cilj ili nije.
Riješenje:
Pomoću gore raspravljene formule možemo izračunati koeficijent korelacije. Tretiranje kamatne stope kao jedne varijable, recimo x, i tretiranje stope inflacije kao druge varijable kao y.

Imamo sve vrijednosti u gornjoj tablici s n = 6.
Unesite sada vrijednosti za izračun koeficijenta korelacije.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Korelacija će biti -

Korelacija = -0,92
Analiza: Čini se da je korelacija između kamatne stope i stope inflacije negativna, što se čini ispravnim odnosom. Kako kamatna stopa raste, inflacija opada, što znači da se teže kretati u suprotnom smjeru, a iz gornjeg rezultata proizlazi da je središnja banka bila uspješna u provedbi odluke vezane uz kamatnu politiku.
Primjer # 3
Laboratorij ABC provodi istraživanje visine i dobi i želio je znati postoji li ikakva veza između njih. Okupili su uzorak od 1000 ljudi za svaku od kategorija i pronašli prosječnu visinu u toj skupini.
Ispod su dati podaci za izračun koeficijenta korelacije.

Trebate izračunati koeficijent korelacije i izvući zaključak da ako postoji bilo kakav odnos.
Riješenje:
Tretiranje starosti kao jedne varijable, recimo x, a tretiranje visine (u cm) kao druge varijable kao y.

Imamo sve vrijednosti u gornjoj tablici s n = 6.
Unesite sada vrijednosti za izračun koeficijenta korelacije.

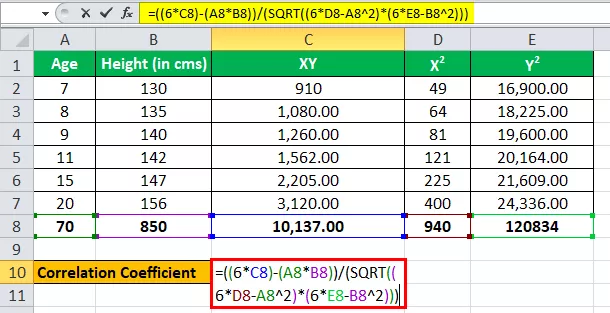
r = (6 * 10.137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1.20.834) - (850) 2 )
r = 1.322,00 / 1.361,23
Korelacija će biti -

Korelacija = 0,971177099
Relevantnost i upotreba
U statistikama se koristi uglavnom za analizu snage odnosa između varijabli koje se razmatraju, a nadalje mjeri i postoji li linearna veza između danih skupova podataka i koliko bi dobro mogle biti povezane. Jedna od uobičajenih mjera koja se koristi u korelaciji je Pearsonov koeficijent korelacije.
Ako se varijabla promijeni u vrijednosti, a zajedno s tom varijablom promijeni vrijednost, tada je razumijevanje tog odnosa presudno jer se vrijednost prve varijable može koristiti za predviđanje promjene vrijednosti druge varijable. Korelacija u današnje moderno doba ima višestruku primjenu, kao što se koristi u financijskoj industriji, znanstvenim istraživanjima i tamo gdje ne. No, važno je znati da korelacija ima tri glavne vrste odnosa. Prvi je pozitivan odnos, koji navodi ako dođe do promjene vrijednosti varijable, tada će doći do promjene povezane promjene u istom smjeru. Slično tome, ako postoji negativan odnos, tada će se povezana varijabla ponašati u suprotnom smjeru. Također, ako nema korelacije, tada će r podrazumijevati nultu vrijednost.Pogledajte slike u nastavku kako biste bolje razumjeli koncept.









