Formula za izračunavanje rente
Pojam "anuiteta" odnosi se na niz periodičnih plaćanja koja će se primati na početku svakog razdoblja ili na kraju razdoblja u budućnosti. Formula za isplatu anuiteta i dospjelu anuitetu izračunava se na temelju PV dospjele anuitete, efektivne kamatne stope i niza razdoblja.
Formula koja se temelji na običnoj anuiti izračunava se na temelju PV obične anuitete, efektivne kamatne stope i nekoliko razdoblja.
Renta = r * PVA redovna / (1 - (1 + r) -n )gdje,
- Obični PVA = Sadašnja vrijednost uobičajene rente
- r = efektivna kamatna stopa
- n = Broj razdoblja
Matematički, jednadžba dospjele rente predstavljena je kao,
Renta = r * PVA zbog / ((1 - (1 + r) -n ) * (1 + r))gdje,
- PVA dospijeće = Sadašnja vrijednost dospjele anuitete
- r = efektivna kamatna stopa
- n = broj razdoblja

Kako izračunati isplatu rente? (Korak po korak)
Izračun isplate rente može se izvesti korištenjem PV uobičajene rente u sljedećim koracima:
- Korak 1 : Prvo odredite PV anuiteta i potvrdite da će se plaćanje izvršiti na kraju svakog razdoblja. Označava se PVA običnim .
- Korak 2: Zatim odredite kamatnu stopu na temelju trenutnog tržišnog povrata. Zatim se efektivna kamatna stopa izračunava dijeljenjem godišnje kamatne stope s brojem periodičnih plaćanja u godini i označava se r. r = Godišnja kamatna stopa / Broj redovnih plaćanja u godini
- Korak 3: Zatim odredite broj razdoblja množenjem broja periodičnih plaćanja u godini i broja godina, a označava se s n. n = broj redovitih plaćanja u godini * Broj godina
- Korak 4: Konačno, anuitetno plaćanje na temelju PV uobičajene anuitete izračunava se na temelju PV obične anuitete (korak 1), efektivne kamatne stope (korak 2) i nekih razdoblja (korak 3), kao što je gore prikazano.
Izračun isplate rente također se može izvesti korištenjem PV anuitete koji treba dospjeti u sljedećim koracima:
- Korak 1: Prvo odredite PV rente i potvrdite da će se plaćanje izvršiti na početku svakog razdoblja. Označava se PVA Due .
- Korak 2: Zatim odredite kamatnu stopu na temelju trenutnog tržišnog povrata. Zatim se efektivna kamatna stopa izračunava dijeljenjem godišnje kamatne stope s brojem periodičnih plaćanja u godini i označava se r. r = Godišnja kamatna stopa / Broj redovnih plaćanja u godini
- Korak 3: Zatim odredite broj razdoblja množenjem broja periodičnih plaćanja u godini i broja godina, a označava se s n. n = broj redovitih plaćanja u godini * Broj godina
- Korak 4: Konačno, anuitetno plaćanje na temelju PV dospjele anuitete izračunava se na temelju PV dospjele anuitete (korak 1), efektivne kamatne stope (korak 2) i nekoliko razdoblja (korak 3), kao što je gore prikazano.
Primjeri
Primjer # 1
Uzmimo primjer Davida, koji je osvojio lutriju vrijednu 10 000 000 dolara. Odlučio se za anuitetno plaćanje na kraju svake godine u sljedećih 20 godina kao opciju isplate. Odredite iznos koji će Davidu biti plaćen kao anuitet ako je stalna kamatna stopa na tržištu 5%.
U nastavku su dati podaci korišteni za izračun anuitetnih plaćanja.
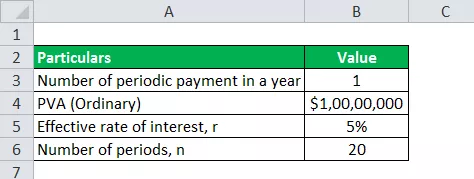
Obični PVA = 10.000.000 USD (od rente koja se plaća na kraju svake godine)
Stoga se izračun rente može izvršiti na sljedeći način -
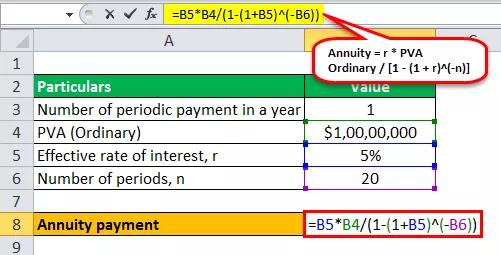
- Renta = 5% * 10.000.000 USD / (1 - (1 + 5%) -20 )
Izračun isplate rente bit će -

- Renta = 802 425,87 USD ~ 802 426 USD
Stoga će David plaćati rente u iznosu od 802.426 USD za sljedećih 20 godina u slučaju uobičajene rente.
Primjer # 2
Uzmimo gornji primjer Davida i odredimo anuitet ako se plaća početkom svake godine sa svim istim uvjetima.
Za izračun rente koristit ćemo iste podatke kao i gornji primjer.
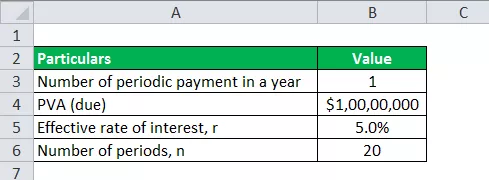
Stoga se izračun rente može izvršiti na sljedeći način -
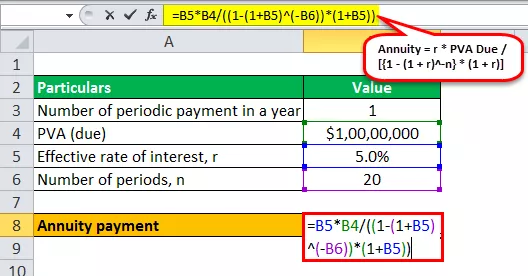
- Renta = r * PVA zbog / ((1 - (1 + r) -n ) * (1 + r))
- Renta = 5% * 10.000.000 USD / ((1 - (1 + 5%) -20 ) * (1 + 5%))
Izračun isplate rente bit će -
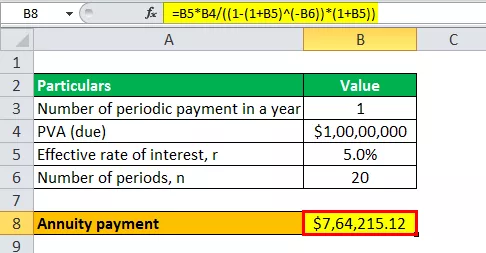
- Renta = 764.215,12 USD ~ 764.215 USD
Stoga će David plaćati rente u iznosu od 764.215 USD za sljedećih 20 godina u slučaju dospijeća rente.
Kalkulator rente
Možete koristiti sljedeći Kalkulator rente.
| Obični PVA | |
| r | |
| n | |
| Formula rente = | |
| Formula rente = | r * |
|
||||||||
| 0 * |
|
Relevantnost i namjene
Isplata rente jedna je od primjena vremenske vrijednosti novca, što je dalje naznačeno razlikom između anuitetnih isplata na temelju redovne rente i dospjelih anuiteta. Donja anuitetna anuitet je da se novac prima na početku svakog razdoblja. Vjeruje se da će se sredstva ulagati na tržište, a u tom će razdoblju zaraditi kamate.
Jednadžba plaćanja anuiteta nalazi primjenu u izračunu anuiteta na dohodak, amortiziranih zajmova, isplata lutrije, strukturiranih nagodbi i bilo koje druge vrste fiksnih periodičnih plaćanja.








