Složena definicija
Kompliciranje je metoda izračunavanja kamatne stope koja je efektivno kamata na kamatu gdje se kamata izračunava na investiciju / početnu glavnicu uvećanu za zarađenu kamatu i ostale reinvestiranja, drugim riječima zarađene kamate akumuliraju se na glavnicu, ovisno o vremenskom razdoblju depozita ili zajma to može biti mjesečno, tromjesečno ili godišnje
Pokušajmo shvatiti što se sastoji i kako to funkcionira kroz neke osnovne primjere
Vrhunska 4 primjera snage složenja
Primjer # 1
I Shane i Mark odlučili su uložiti 1.00.000 američkih dolara, ali Shane je odlučio uložiti u jednostavne kamate, dok Mark deset godina ulaže u složene kamate s 10% kamate. Da vidimo što će se dogoditi nakon deset godina.
Riješenje:
Dakle, izračun Shaneove investicije bit će -

Ukupni iznos zarade = 200.000 USD
Jednostavnim kamatama, Shane će nakon 10 godina dobiti 2.000.000 USD.
Izračun ulaganja u marku bit će -

Ukupni iznos zarade = 2,59,374 USD
Uz složene kamate, Markove vrijednosti ulaganja narast će na 2,59,374 USD.
Sada je Shane odlučio investirati metodama složenja poput Marka, a obojica su uložila 2.000.000 USD po stopi od 15%.
Izračun Shaneove investicije bit će -

Ukupni iznos zarade = 8,09,111.55 USD
Shane ostaje uložen 10 godina i dobiva konačni iznos od 8,09,111.55 USD po stopi od 15%.
Izračun ulaganja u marku bit će -

Ukupni iznos zarade = 65,83,790.52 USD
Međutim, Mark je dugoročni ulagač strpljenja i ostaje uložen 25 godina, a vrijednost njegove investicije raste na 65,83,790.52 USD
Gornji primjer pokazuje snagu smjese. Što je horizont ulaganja dulji, to je veći eksponencijalni rast.
Primjer # 2 (tjedno)
Simon ima uštedu od 7500 američkih dolara, a za fond svog sina koji će pohađati fakultet nakon 15 godina, odlučio je ulagati u američke štedne obveznice. Simonov cilj je uštedjeti 20.000 USD, a godišnja postotna stopa američke štedne obveznice je 6%. Koja je buduća vrijednost Simon Money-a nakon 15 godina?
Riješenje:
S obzirom,
- Glavnica = 7500 USD
- Stopa = 6% ili 0,06
- Vremensko razdoblje = 15 godina.
- Koliko se puta složi u godini n = 52 tjedna
- Buduća vrijednost =?
Dakle, izračun buduće vrijednosti bit će -

Formula za tjedno sastavljanje je kao u nastavku.
F = P (1 + r / n) n * t- F = 7500 USD (1 + 0,06 / 52) 52 * 15
- F = 7500 USD (1 + 0,001153846) 780
- F = 18.437,45 USD
Dakle, iz gornjeg izračuna, jasno je da Simonov cilj da uštedi 20,00 USD neće biti postignut gore navedenim metodama, ali bliži je tome.
Metoda kontinuiranog spajanja
Pokušajmo sada s gornjim primjerom s Formulom kontinuiranog složenja.
Dakle, izračun buduće vrijednosti bit će -

- F = 7500e 0,06 * 15
- F = 7500 e 0,9
- Buduća vrijednost (F) = 18.447,02 USD
Sada čak i uz Kontinuirano kombiniranje, Simonov cilj neće uštedjeti 20 000 američkih dolara za fakultetski fond svog sina.
Idemo vidjeti s mjesečno sastavljenom formulom koliko je novca Simon trebao uložiti da postigne svoj cilj uštede 20.000 američkih dolara u 15 godina s godišnjim tranšem od 6%?
Dakle, izračun buduće vrijednosti bit će -
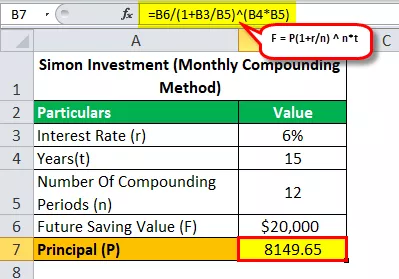
- 20 000 USD = P (1 + 0,06 / 12) 12 * 15
- P = 20.000 USD / (1 + 0,06 / 12) 12 * 15
- Glavnica (P) = 8149,65
Dakle, rješavanjem gornje jednadžbe, dobit ćemo odgovor koji iznosi 8.149,65 USD (Iznos koji Simon treba uložiti da bi postigao svoj cilj uštede 20 000 USD za 15 godina).
Primjer # 3 (efektivni godišnji prinos)
Recimo, XYZ ograničena banka daje 10% godišnje starijim građanima za fiksni depozit, a mi ovdje pretpostavljamo da su kamate u bankama tromjesečno složene kao i sve ostale banke. Izračunajte efektivni godišnji prinos za 5, 7 i 10 godina.
Riješenje:
Godišnji prinos za 5 godina:
- t = 5 godina
- n = 4 (tromjesečno složeno)
- I = 10% godišnje
Dakle A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 za 5 godina
Efektivna kamata = 0,6386 / 5
Efektivni I = 12,772% godišnje
Godišnji prinos za 7 godina:
- t = 7 godina
- n = 4 (tromjesečno složeno)
- I = 10% godišnje
Dakle A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- I = 1,9965 za 7 godina
- Efektivno I = 0,9965 / 7
Efektivni I = 14,236% godišnje
Godišnji prinos za 10 godina:
- t = 10 godina
- n = 4 (tromjesečno složeno)
- I = 10% godišnje
Dakle, A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1,685 za 10 godina
- Efektivno I = 1.685 / 10
Efektivni I = 16,85% godišnje
Primjer # 4 - (Renta: buduća vrijednost)
Ulaže se 1000 dolara svaka 3 mjeseca po 4,8% godišnje složeno kvartalno. Koliko će vrijediti renta za 10 godina?
Riješenje:
Dakle, kada kažemo koliko će renta vrijediti za 10 godina, ovdje moramo pronaći buduću vrijednost, a to je važno jer kad god postoji primjer anuiteta, moramo vidjeti što moramo saznati.
Dakle, formula buduće vrijednosti je
FV rente = P ((1+ r) n - 1 / r)- P = povremeno plaćanje
- r = stopa po razdoblju
- n = Broj razdoblja
Dakle, formula buduće vrijednosti je
- Dakle, ovdje P = 1.000 USD
- r = 4,8% godišnje ili 0,048
- r (tromjesečno) = 0,048 / 4
- r (tromjesečno) = 0,012
- n = 10 godina
- n (Broj primjenjivanja složenja) = 10 × 4 = 40
Dakle, izračun FV rente bit će -

Dakle, sada je FV = 1000 USD (1 + 0,012) 40 -1 / 0,012)
Dakle, rješavanjem gornje jednadžbe dobit ćete FV od 50.955,30 USD
Dakle, kolika će biti renta za 10 godina i odgovor je 50.955,30 USD
Kao dodatak, također iz gornjeg primjera možemo saznati koliko se kamata zaradi u 10 godina.
Kako se ulaže 40 puta 1000 dolara, to je ukupno ulaganje (40 × 1000 američkih dolara = 40 000 američkih dolara).
Dakle, kamata = buduća vrijednost - ukupna investicija
- Kamate = 50.955,30 - 40.000 dolara
- Kamate = 10.955,30 američkih dolara
Dakle, ovdje je važno shvatiti da u anuitetima investitori mogu zaraditi velik interes. U gornjim konkretnim primjerima, polog od 40 000 USD daje zauzvrat ukupnu kamatu od 10 955,30 USD.
Napomena: Možete preuzeti gore navedeni Excel obrazac za detaljan izračun.








